SAT数学，到底考啥呢？首先，请出官方“说明书”。

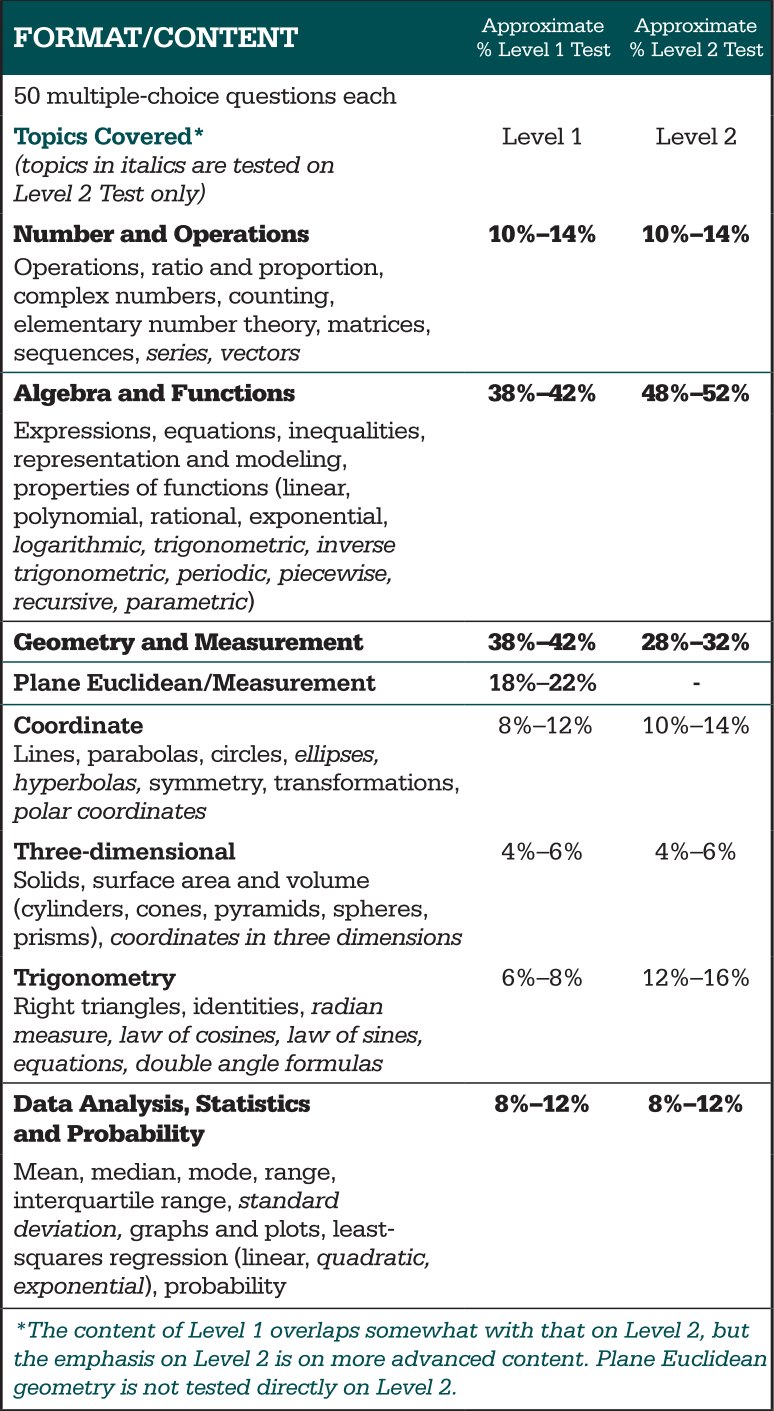
　　从官方大纲中我们不难发现，大体上，SAT数学包括number and operations数学运算（分数占比10%-14%），algebra and function代数与方程（分数占比38%-42%），geometry and measurement几何与度量（分数占比18%-22%），data analysis, statistics and probability统计与概率分析（分数占比8%-12%）四个方面。

　　落实到细节层面，对于各位考生来说，SAT数学涵盖的范围，基本上近似于初中到普高高一的数学内容。

　　这也就是为什么在备考阶段，许多朋友次拿到SAT数学真题时，有种：就这？这还要计算器？等等，这就没啦？的想法涌上心头，特别是对于阅读稍差的朋友而言，更是会有种“与其说我在做数学，不如说我在做阅读理解，数学只是附带的”感觉。

　　这也会让备考的各位感觉数学，洒洒水啦，临考看一看，满分简简单的“幻想”。然而，当各位真正刷完套完整的SAT数学真题，特别是对完答案后，能真正保证全对，满分的却几乎没有。

　　事实上，即使是系统复习过的，刷过许多题的老手们，也没几位能保证每次数学都能做全对。这就出问题了，明明知识点都知道，为何总是会做错那么=random（1，58）道题呢？

　　大多数朋友对完答案后，对于错题的反应都是：“啊我瞎了，啊我看错了，啊这。。。”，然后就书一合，深刻检讨，下次再犯。每个人容易看错，理解错的点都是不一样的，所谓“正确答案只有一个，但做错的脑回路可以有上万个”。

　　学而不思则罔，思而不学则殆，缺少自我纠错的过程，就很有可能会在同一个点上，反复犯错。所以今天，我们就着重介绍一个，可能是各位都容易“一疏忽”就看错的知识点吧！

　　SAT数学在最基本的number and operations数学运算这里，特别喜欢去考察单位的换算。

　　美国作为世界上唯三仍普遍使用英制单位的国家（另外两国为缅甸和利比里亚，是的你没看错，没有英国），公制单位与英制单位之间和公制单位内部的单位换算，以成为日常生活中不可避免的一环，因此在SAT数学的试卷里，单位换算相关的题目时有出现。

　　相对而言，没什么坑的题目，还是很好识别的，比如2016年5月北美卷的这道题目：

　　3 To make a bakery's signature chocolate muffins, a baker needs 2.5 ounces of chocolate for each muffin. How many pounds of chocolate are needed to make 48 signature chocolate muffins?(1 pound = 16 ounces)A) 7.5B) 10C) 50.5D) 120

　　简言之，做一个经典松饼要用2.5盎司的巧克力，问做48个经典松饼需要多少磅的巧克力？

　　看！多贴心的官方，普普通通的一道题，为了防止各位计算时没看到这里问的是磅数，而不是题干一开始给出的盎司，还在pounds这加了下划线！如果这样，各位在做题时仍然直接用2.5*48=120 ounces，然后大手一挥，D选上。

　　这就真的只能怪你看题目不仔细了，也即在下次遇到出现各种单位表达时，一定要看清楚最后结果要求的是什么单位。

　　当然，不是每次都是这么平铺直叙的告诉你，我要换算单位了！偶尔，挖个小小的坑，还是有不少人会掉进去的，比如同样这张卷子的最后一题：

　　# Ms Simon’s Workday Morning Drive

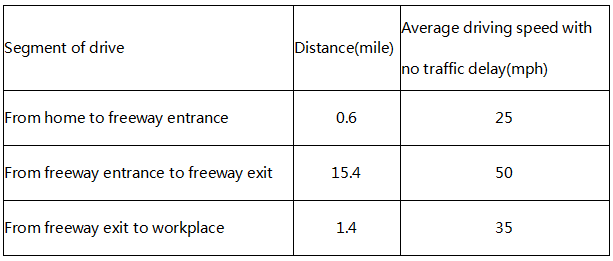
　　Ms. Simon drives her car from her home to her workplace every workday morning. The table above shows the distance, in miles, and her average driving speed, in mile per hour(mph), when there is no traffic delay, for each segment of her drive.

　　37. One morning, Ms. Simon drove directly from her workplace in 24 minutes. What was her average speed, in miles per hour, during her drive that morning?

　　38. If Ms. Simon starts her drive at 6:30 a.m., she can drive at her average driving speed with no traffic delay for each segment of the drive. If she starts her drive at 7:00 a.m., the travel time from the freeway entrance to the freeway exit increases by 33% due to slower traffic, but the travel time for each of the other two segments of her drive does not change. Based on the table, how many more minutes does Ms. Simon take to arrive at her workplace if she starts her drive at 7:00 a.m. than if she starts her drive at 6:30 a.m.?(Round your answer to the nearest minute.)

　　很简单的一张表格，记录了西蒙女士早晨的通勤流程，从家到高速公路入口有0.6英里的路程，平均时速在25英里每小时。

　　高速公路入口到出口有15.4英里的路程，时速50英里每小时，从出口到工作地点，1.4英里，平均时速35英里每小时。表格内的数据为没有交通堵塞的情况。

　　37题问我们，有一天早晨，西蒙女士花费了24分钟，从家到工作地点，问平均时速是多少？单位：英里每小时。

　　首先根据表格，总路程为0.6+15.4+1.4=17.4英里。花费的时间为24分钟，可单位是小时，所以需要换算一下，也即24min=24/60=0.4小时。

　　所以平均速度=路程/时间=17.4/0.4=43.5英里每小时。这我相信各位都没什么问题。

　　容易出错的是38题，西蒙女士如果早晨是6:30出的门，一路不会有耽搁。但如果是7点出门，则在高速公路上花费的时间会因为堵车，多33%，其他部分不会发生变化。问我们7点出门比6:30出门晚多少分钟？取整数位分钟。

　　看到了吧！不管是表格也好，37题也罢，大家的时间单位都是小时，但在38题，这里问的是分钟。

　　特别又是最后一题，这时候很多朋友注意力就已经有些松懈了，突然试卷摆了一道：题目给的是小时，问的是分钟。这就造成了很多朋友这里最后忘记乘以60，也即小时与分钟的换算了，所以这题应该是这么解的：

　　由于前后两段时间没有耽搁，所以整体耽误的时间也即在高速公路上耽搁的时间，由时间=路程/速度，得：0.33*（15.4/50）=0.10164小时。别急，还有一步，这算出来的，可是小时哦！

　　所以最后答案为：0.10164*60=6.0984分钟，取整后得到答案为：6分钟。这就是关于一个最简单的，一个单位换算，在SAT当中可能会给各位挖的坑。其实回头看看，都很小儿科。

　　考官为了防止我们跑偏了一般还会画个下划线，提醒下各位。但是，真正在做题时，这个点出错的人还真有不少，特别是这种最后一两题，前面是一种单位，后面换了另外一种单位的题目。

　　当然，单位换算只是各位容易马虎出错的一个小点而已，在整体复习的过程中，这样的小点还有很多，这也就是为何建议各位整个错题集，记录下容易出错的点，的原因。毕竟，因为这种疏忽被扣分，可是很让人心痛的，不是吗 ?

       更多关于sat考试的个性化问题敬请咨询新航道官网