A-Level数学P4

　　2021年1月考情分析

　　考试日期：2021年1月07日

　　考试时长：1小时30分

　　01

　　本题考查了P4的第4章二项式展开。

　　a问）常规题，先将常数项化成1，然后利用二项式展开的公式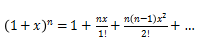将式子写成多项式的形式，或者可以直接套用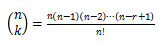将题目所给式子直接展开。题目要求写前四项，所以答案需要写成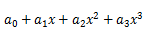的形式。

　　b问）借助a问的结果算出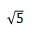的近似值，这是二项式展开的常考题型，答题时需注意直接代入时所得到的是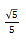的值，要得到最后答案应该乘以5。

　　类似真题：

　　Oct 2020 Q2

　　02

　　本题考查了P4的第7章向量。

　　a问）求两个向量所形成的夹角度数。需要注意两个细节：一个两个向量的方向，需要保持一致，同时指向一个点或者同时从一个点出发；第二个是单位，题目要求角度制。

　    b问）求平行四边形的面积，使用P1的公式。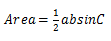

　　求出三角形的面积，然后再乘以2。

　　03

　　本题考查了P4的第1章证明。这道题是课本上例题的原题，要求考生用反证法证明：没有的奇数。在官考中出现课本上的例题是非常罕见的，所以这道题分值不高，只有2分。只要好好准备，这道题拿满分不成问题。

　　04

　　本题考查了P4的第5章参数方程。

　　a问）已知函数的参数方程表达，求函数的笛卡尔方程。考生可以采用代入法，用含有x的式子表达t，然后再代入y 中，化简成关于x的式子。方法不难，主要是化简的时候需要用到P3分式化简的知识，考生一定注意不要自己发明化简的法则。

　　b问）是P3的一个知识点：函数的值域，考生需要能够求根据a问的domain求出函数的range。

　　05

　　本题考查了P4的第6章积分。这道题需要考生用换元的方法求积分的精确值，并且将答案写成题目要求的形式。需要注意在计算定积分时不要忘记替换limit。题目直白，难度不大。

　　06

　　本题考查了P4的第5章隐函数求导。

　　a问）用x和y表达出dy/dx。

　　b问）先求函数和y轴的交点，然后求出过该点的法线方程。这是隐函数的常规考法，以往的试卷和课后题都有较多的相同类型的题目。需要注意的是求导过程中chain rule和product rule的使用。

　　07

　　本题考查了P4第6章积分的内容。

　　a问）考查了分部积分。这是课本例题的一个变形，主要是在分部积分的过程中，积分主体重复出现，考生需要将要求的积分看作一个整体进行计算。

　　b问）求函数和x轴所围成的面积。先求出函数和x轴的交点作为upper and lower limit，然后代入上问求出的积分中，就能得到题目要求的形式。

　　08

　　本题考查了P4第7章向量。本次考试的第二道向量题，难度也不大。证明两条直线是异面的关系。通过x和y坐标相等求出λ和μ的值，然后代入z坐标即可。

　　09

　　本题考查了P4的第6章积分。考生需要求参数方程围绕x轴旋转360°之后所围成的图形的体积，利用公式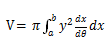

　　得出最后的结果，并将结果的精确值用题目所要求的形式写出来。首先考生需要先通过三角求出函数图像和x轴的交点，然后利用三角函数的恒等公式证明出a问要求的式子。b问在上一问的基础上求出积分的精确值。本题积分的解法难度不是太大。

　　10

　　本题考查了P4第6章积分，微分方程的内容。以应用题的形式，题目表达不是很难。没有和相关变化率的知识一起考查，从一定程度上降低了难度。

　　a问）考查partial fraction，难度不大，为后面做铺垫。

　　b问）题目给出微分方程以及初始条件，学生可以采用分离变量法证明出H的表达式。

　　c问）需要求出当H=8的时候，t的值是多少，可以代入到上一问求出的式子中。

　　d问）需要求出H的表达式的limit，这个是P3的一个常考点，分式函数的range。

　　类似真题：

　　Oct 2020 Q9

　　小结

　　本次P4考试较为简单，难度相比2020年10月的P4考试有所降低。微分和积分仍然是考查重难点，但是计算量不大，问题都很直接，没有需要技巧的新题。平时授课和练习过程中，学生掌握不是很牢固的证明题本次考试竟然出了课本的例题，并且分值只有两分，这在以往的考试中是没有出现过的，相信在今后的考试中也不太有可能再次出现。还有向量部分，很久没有出现的求平行四边形的面积的题目又“重出江湖”，披着P4的外衣实则考的是P1的知识点。

　　考试难度不大，更加需要注意做题的规范性和计算的准确，避免在不必要的地方丢分，从而与A*失之交臂。

       更多关于出国留学考试的个性化问题敬请咨询新航道官网