A-Level数学P1 2021年1月考情分析
阅读量:
A-Level数学P1
2021年1月考情分析
考试日期:2021年1月11日
考试时长:1小时30分
01
本题考查第8章differentiation有关导数求解、导数的图像意义及应用等考点。须通过导数求得原函数在垂足处的斜率后,再根据垂线与原函数斜率关系求得垂线方程。可直接套用书上公式,属于常规问题。
02
与2019年10月份官考第2题神似,主要考查考生基本的方程求解能力以及应用题读题理解能力。只需将两组x、y值代入方程求解参数即可,属于简单题。
03
本题考查图像变换以及三角函数图像,与2020年1月份官考第7题神似。
a问)对cosine函数图像进行了stretching变形,已知变形过程,求变形结果。
b问)在a问的基础上进行了translation变形,已知变动结果,反推变形过程。本题需要学生对三角函数图像的精确记忆,以及函数图像变换相关知识的熟练掌握。
04
本题考查知识点较多,包括straight line、quadratics以及inequalities的相关内容。
a问)已知两点坐标求过两点直线解析式,直接代公式求解即可。
b问)已知抛物线顶点和线上另一点坐标,求抛物线解析式,可以通过抛物线顶点坐标公式或对称轴坐标公式直接解方程组得到答案。
c问)考查不等式组的几何意义,列出正确不等式来定义阴影区域。本题综合性较强,考点属于常见类型。
05
本题是对radians、trigonometric ratio相关内容的考查。需要学生熟练运用sector面积公式、triangle面积公式、sine rule以及length of arc公式。其中第a问采用sine rule求未知角时应注意角度取值(钝角而非锐角)。
06
本题考查了第4章的反比例函数图像及图像转换,已知两条曲线解析式交点个数、以及二次不等式的求解。
a、b问)要求画出stretching、translation变换后的反比例函数图像,并标出渐近线和与坐标轴交点。
c问)可通过联立解析式,并令discriminant小于0,通过求解二次不等式来求解参数k的取值范围。本题亦比较综合,知识点较多。
07
本题主要考查方程求解以及一阶导、二阶导等考点。
a问)可采用换元法,将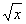
看作一个未知量,从而将原方程转换为一元二次方程求解。
b问)求解二阶导,属于微分计算最基本操作。
08
本题考查三次函数解析式及图像以及二次函数求解。问法比较灵活,需要学生对解析式及相应图像理解透彻,并熟练运用。本题基本上都在因式分解和脱括号,比较考验基本功,只要能正确理解题目意图,并保证计算不出错,本题不难得分。
09
本题考查积分的计算。
a问)学生需要用到第1章index law的部分知识对函数式进行化简变形,然后求不定积分。
b问)解带参数的函数关系式,需要根据题目中给出的关系条件,列多个方程形成方程组并求解。本题比较常规,主要考查计算。
小结
总体来说,本次考试难度依然保持稳定,多个题目与之前的真题相近或神似。与上次考试一样,本次试卷中与函数图像和图像变换相关的题目依然较多,其中直接考查图像的问题达到10分以上,其他题目通过图像提问或表示的亦不在少数,由此可以看出,深刻理解函数与其图像的联系在本单元考试中显得较为关键。另外,本次考试中与带参数的表达式相关的问题略多,需要通过方程组求解,这种稍显抽象的题目更要求对知识点的灵活掌握。
更多关于出国留学考试的个性化问题敬请咨询新航道官网
