今天来一起讨论S2中的f(x)和F(x)。首先，我们先来看一下它们的定义解释。

　　小f(x)是probability density function，概率密度函数，简称PDF，用来描述continuous random variables(连续性随机变量)的输出值，在某个确定的取值点附近的概率大小的函数。大F(x)是cumulative distribution function，累积分布函数，简称CDF，用来描述连续性随机变量的概率分布。

　　了解完定义后，接着我们来看一幅概率分布图。

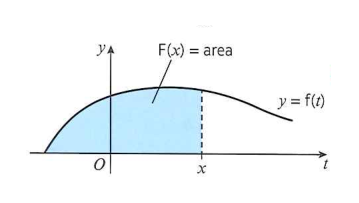
　　图中黑色线条f(x)就是我们的CDF，该方程与x轴围成的面积代表着概率。

　　图中蓝色的部分就是F(x)，代表着变量x在不同值的时候概率的变化。

　　根据图片，我们来讨论一下什么样的方程才可以成为PDF?

　　因为PDF代表着概率分布，所以一定要大于

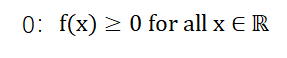
　　又因为概率永远在0(0%，完全不可能发生)到1(100%，一定会发生)之间，所以总概率为

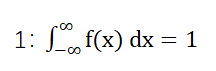
　　同时满足这两个条件，则方程可以作为PDF。

　　结合我们S1学习的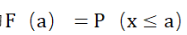对于一个方程求与x轴之前的面积，就是对于f（x）进行积分。所以

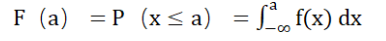
　　简单的概括就是F是f的积分，f是F的微分(求导)。

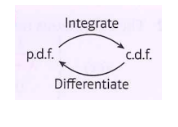
　　看完f和F的关系，下一步就是如何具体实现两者之间的转换。

　　一个标准的PDF至少是二段函数，如

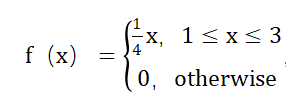
　　下面半段是指在其他的非变量取值区间，概率都是0。

　　积分转化方法有两种：定积分法、不定积分法

　　不定积分法

　　Step1直接对f(x)进行积分

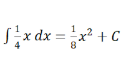
　　Step2 代值求C，可带入下限f(1)=0或者上限f(3)=1，求出

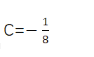
　　Step3完成

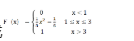
　　PS：注意格式，F(x)一定比f(x)多一行。

　　定积分法

　　(注意定积分需要带入上下限，而我们需要通过定积分得到一个方程，所以把上限设为x)

　　Step1对f(x)进行积分，为避免与上限的x重复，我们把方程的未知数变为t

　　Step2

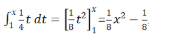
　　这样就可以直接得到方程

　　Step3完成格式

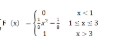
　　那么，这就是我们关于二段PDF和三段CDF的转化的全部内容啦!

　　是不是很简单呀?同学们赶快实操起来吧!