A-Level数学篇:三步法求导复合函数
2022-02-25 16:12
作者 :
阅读量:
在A-Level Pure Mathematics 3第六章中,我们第1次接触chain rule (链式法则),它是微积分求导方法之一,用于复合函数的求导,公式为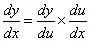 。
。
复合函数的导数将是构成复合这有限个函数在相应点的导数的乘积,就像锁链一样一环套一环,故称链式法则。笔者对于2017-2020真题分析后,发现运用链式法则解题的考察频率接近15%,无论出题频率还是分值占比都非常高,所以考生们需要引起足够重视。
首先,我们一起回顾一下在P1中所学习的导数运算。
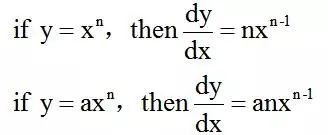
但是根据以往所学你会发现依然无法做出下面↓这道例题,那么很心酸7分就这么舍你而去了。
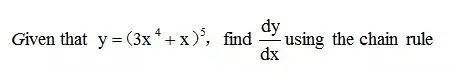
原因何在呢?
是因为这道题是针对复合函数进行求导,需要利用chain rule来进行解题。
划重点!!!
chain rule是针对复合函数的求导,所以应用该法则最根本还是掌握复合函数的分解。
那么接下来,我们就一起练习如何把复合函数分解成多个初等函数。
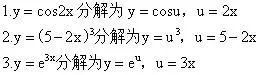
掌握了复合函数分解之后,现在我们就可以来学习如何利用三步法对于该函数进行求导了。
示例:
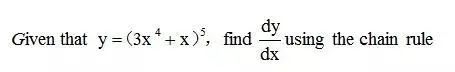

再次划重点!!!
第三步一定不要忘记把x替换中间变量u的表达式。下图即为复合函数求导三步法,大家一起来复习下。

最后归纳总结,chain rule就是对复合函数进行微分的方法。导数的知识点从P1到P4都有涉及,考察频率之高大家需要精 准掌握如何利用三步法chain rule对函数进行求导,才能取得理想好分数。
上一篇:
A-Level数学篇:导数中的乘法法则
下一篇: A-level基础数学的评分标准
